Draw Bfs Tree Given Undirected Graph

Breadth-First Traversal (or Search) for a graph is similar to Breadth-First Traversal of a tree (See method 2 of this post). The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array. For simplicity, it is assumed that all vertices are reachable from the starting vertex.

For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don't mark visited vertices, then 2 will be processed again and it will become a non-terminating process. A Breadth-First Traversal of the following graph is 2, 0, 3, 1.

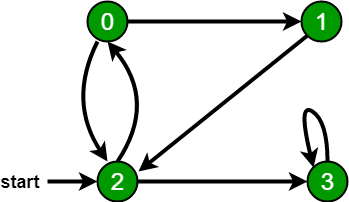
Following are the implementations of simple Breadth-First Traversal from a given source.
The implementation uses an adjacency list representation of graphs. STL's list container is used to store lists of adjacent nodes and the queue of nodes needed for BFS traversal.

C++

#include<bits/stdc++.h>

using namespace std;

class Graph

{

int V;

vector<list< int >> adj;

public :

Graph( int V);

void addEdge( int v, int w);

void BFS( int s);

};

Graph::Graph( int V)

{

this ->V = V;

adj.resize(V);

}

void Graph::addEdge( int v, int w)

{

adj[v].push_back(w);

}

void Graph::BFS( int s)

{

vector< bool > visited;

visited.resize(V, false );

list< int > queue;

visited[s] = true ;

queue.push_back(s);

while (!queue.empty())

{

s = queue.front();

cout << s << " " ;

queue.pop_front();

for ( auto adjecent: adj[s])

{

if (!visited[adjecent])

{

visited[adjecent] = true ;

queue.push_back(adjecent);

}

}

}

}

int main()

{

Graph g(4);

g.addEdge(0, 1);

g.addEdge(0, 2);

g.addEdge(1, 2);

g.addEdge(2, 0);

g.addEdge(2, 3);

g.addEdge(3, 3);

cout << "Following is Breadth First Traversal "

<< "(starting from vertex 2) \n" ;

g.BFS(2);

return 0;

}

Java

import java.io.*;

import java.util.*;

class Graph

{

private int V;

private LinkedList<Integer> adj[];

Graph( int v)

{

V = v;

adj = new LinkedList[v];

for ( int i= 0 ; i<v; ++i)

adj[i] = new LinkedList();

}

void addEdge( int v, int w)

{

adj[v].add(w);

}

void BFS( int s)

{

boolean visited[] = new boolean [V];

LinkedList<Integer> queue = new LinkedList<Integer>();

visited[s]= true ;

queue.add(s);

while (queue.size() != 0 )

{

s = queue.poll();

System.out.print(s+ " " );

Iterator<Integer> i = adj[s].listIterator();

while (i.hasNext())

{

int n = i.next();

if (!visited[n])

{

visited[n] = true ;

queue.add(n);

}

}

}

}

public static void main(String args[])

{

Graph g = new Graph( 4 );

g.addEdge( 0 , 1 );

g.addEdge( 0 , 2 );

g.addEdge( 1 , 2 );

g.addEdge( 2 , 0 );

g.addEdge( 2 , 3 );

g.addEdge( 3 , 3 );

System.out.println( "Following is Breadth First Traversal " +

"(starting from vertex 2)" );

g.BFS( 2 );

}

}

Python3

from collections import defaultdict

class Graph:

def __init__( self ):

self .graph = defaultdict( list )

def addEdge( self ,u,v):

self .graph[u].append(v)

def BFS( self , s):

visited = [ False ] * ( max ( self .graph) + 1 )

queue = []

queue.append(s)

visited[s] = True

while queue:

s = queue.pop( 0 )

print (s, end = " " )

for i in self .graph[s]:

if visited[i] = = False :

queue.append(i)

visited[i] = True

g = Graph()

g.addEdge( 0 , 1 )

g.addEdge( 0 , 2 )

g.addEdge( 1 , 2 )

g.addEdge( 2 , 0 )

g.addEdge( 2 , 3 )

g.addEdge( 3 , 3 )

print ( "Following is Breadth First Traversal"

" (starting from vertex 2)" )

g.BFS( 2 )

C#

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

class Graph{

private int _V;

LinkedList< int >[] _adj;

public Graph( int V)

{

_adj = new LinkedList< int >[V];

for ( int i = 0; i < _adj.Length; i++)

{

_adj[i] = new LinkedList< int >();

}

_V = V;

}

public void AddEdge( int v, int w)

{

_adj[v].AddLast(w);

}

public void BFS( int s)

{

bool [] visited = new bool [_V];

for ( int i = 0; i < _V; i++)

visited[i] = false ;

LinkedList< int > queue = new LinkedList< int >();

visited[s] = true ;

queue.AddLast(s);

while (queue.Any())

{

s = queue.First();

Console.Write(s + " " );

queue.RemoveFirst();

LinkedList< int > list = _adj[s];

foreach ( var val in list)

{

if (!visited[val])

{

visited[val] = true ;

queue.AddLast(val);

}

}

}

}

static void Main( string [] args)

{

Graph g = new Graph(4);

g.AddEdge(0, 1);

g.AddEdge(0, 2);

g.AddEdge(1, 2);

g.AddEdge(2, 0);

g.AddEdge(2, 3);

g.AddEdge(3, 3);

Console.Write( "Following is Breadth First " +

"Traversal(starting from " +

"vertex 2)\n" );

g.BFS(2);

}

}

Output

Following is Breadth First Traversal (starting from vertex 2)  2 0 3 1          

Time Complexity: O(V+E), where V is the number of nodes and E is the number of edges.
Auxiliary Space: O(V)

Illustration :

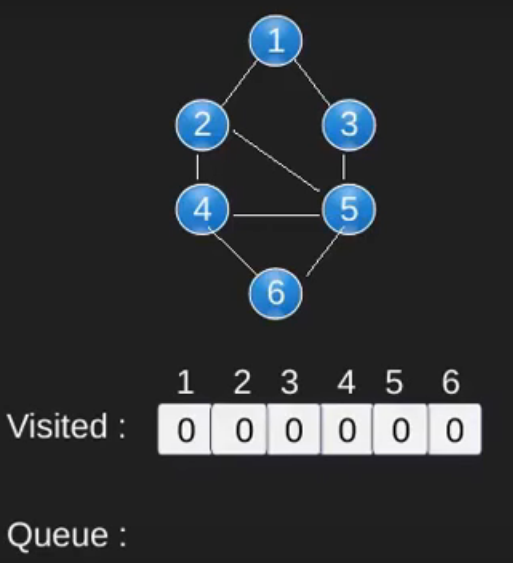
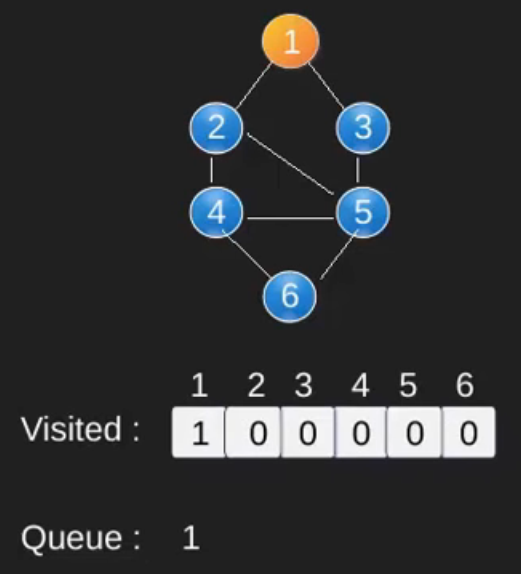
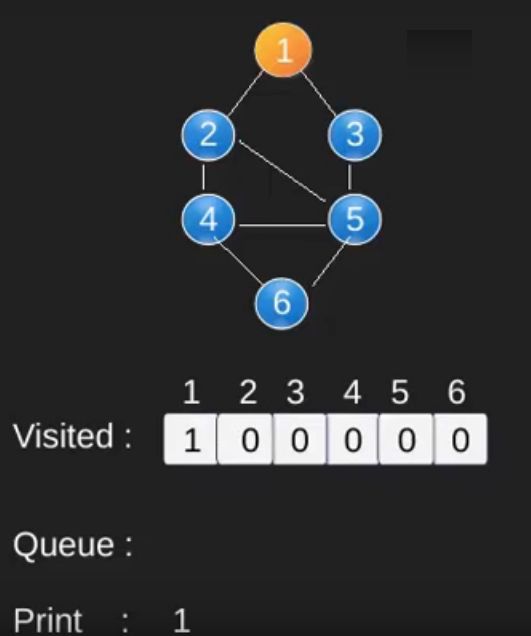
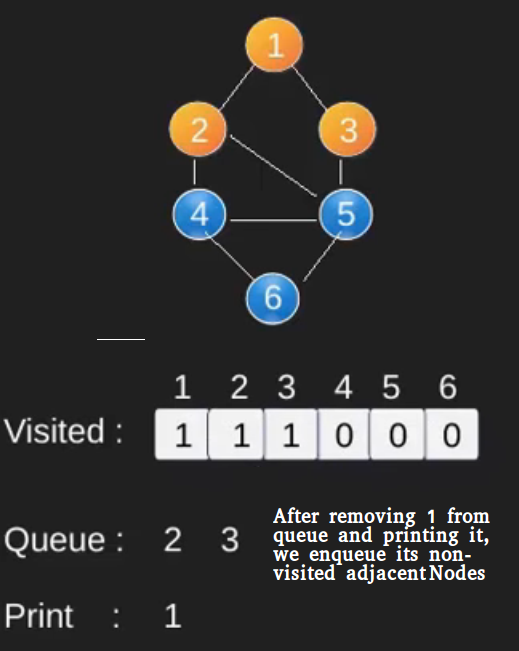
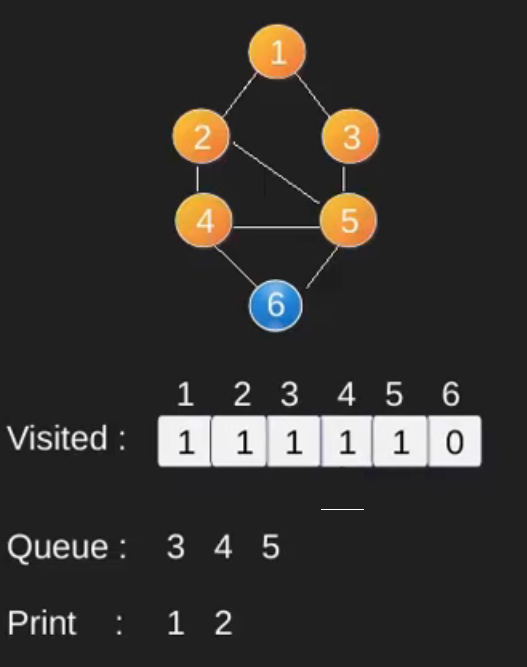
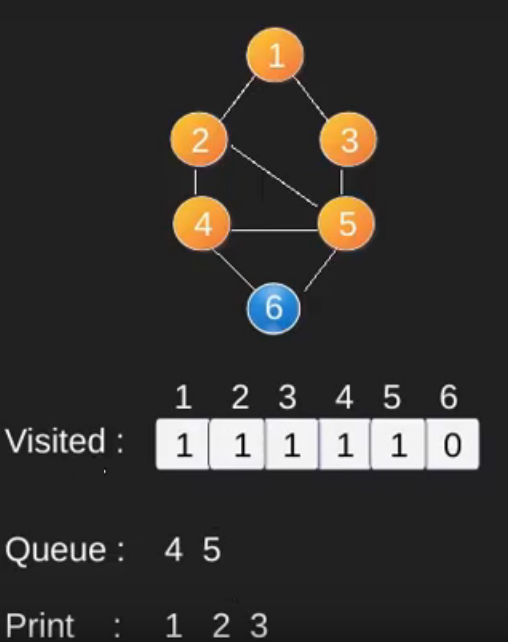
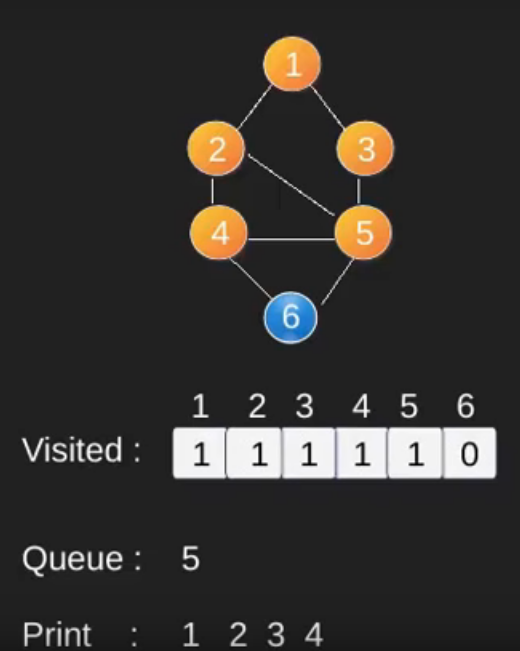
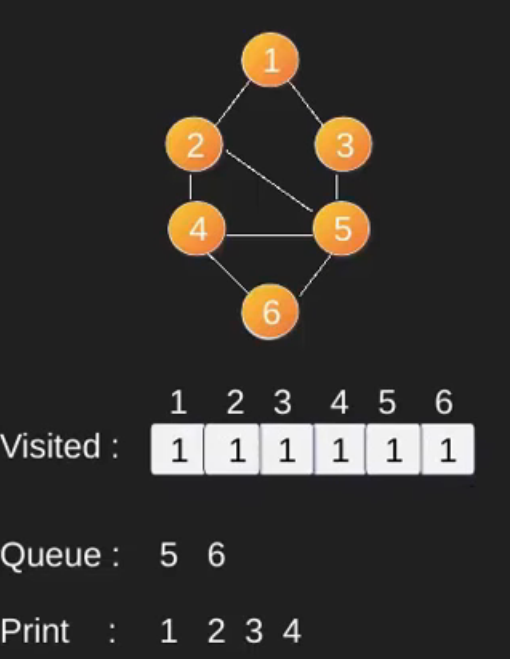
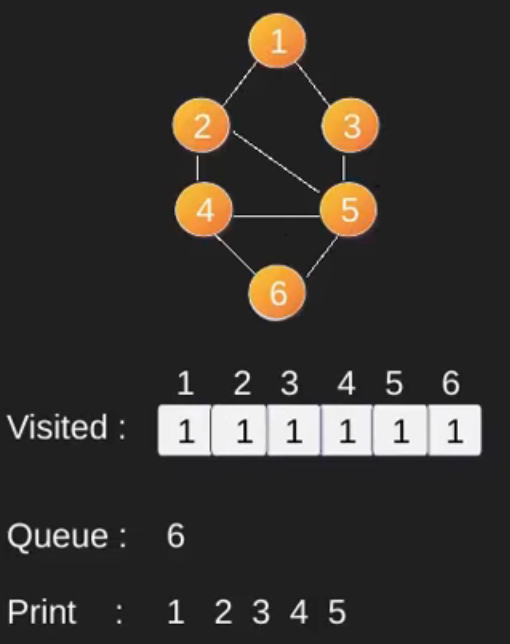
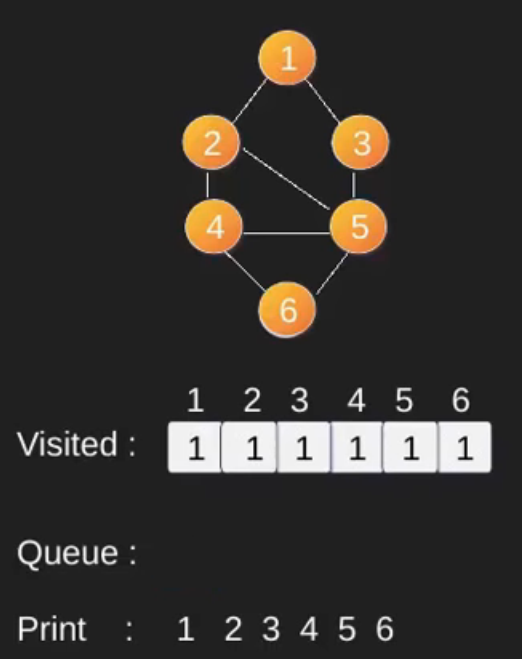
Note that the above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex (for example Disconnected graph).

To print all the vertices, we can modify the BFS function to do traversal starting from all nodes one by one (Like the DFS modified version).

The C++ code for BFS traversal for entire graph (valid for directed as well as undirected graphs) with possible multiple disconnected components is as follows:

C++

vector< int > bfsOfGraph( int V, vector< int > adj[])

{

vector< int > bfs_traversal;

vector< bool > vis(V, false );

for ( int i = 0; i < V; ++i) {

if (!vis[i]) {

queue< int > q;

vis[i] = true ;

q.push(i);

while (!q.empty()) {

int g_node = q.front();

q.pop();

bfs_traversal.push_back(g_node);

for ( auto it : adj[g_node]) {

if (!vis[it]) {

vis[it] = true ;

q.push(it);

}

}

}

}

}

return bfs_traversal;

}

You may like to see below also :

• Recent Articles on BFS
• Depth First Traversal
• Applications of Breadth First Traversal
• Applications of Depth First Search

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

sullivanseessishe.blogspot.com

Source: https://www.geeksforgeeks.org/breadth-first-search-or-bfs-for-a-graph/

Share this post